- Published on
SQL索引剖析[译]
- Authors

- Name
- Leon
本文翻译自《SQL Performance Explained》之“Chapter 1, Anatomy of an SQL Index”。
“索引使查询更快”是我曾见到过的对索引的最基本解释。尽管它很好地描述了索引最重要的一面,但不幸地是,并不足以体现本书。本章以不是那么肤浅的方式来描述索引结构,但也不会深挖细节。它为本书中讨论的SQL性能方面提供足够的洞察力。
索引是使用create index语句在数据库中建立的一个不同的数据结构。它需要自己的磁盘空间来保存索引表数据的副本。这意味着索引是纯粹的冗余。创建索引并不会改变表数据;它只是创建了一个指向表的新的数据结构。总之,一个数据库索引非常像一本书末尾处的索引:它占有自己的空间,完全冗余,指向存储在另外一个不同地方的实际信息。
聚簇索引
SQL Server 和 MySQL(使用InnoDB)更广泛地看待索引的含义。它们指那些由索引结构(仅为聚簇索引)构成的表。这些表在Oracle数据库中称为索引组织表(IOT)。Chapter 5, “Clustering Data”,将更详细地描述它们并解释它们的优点和缺点。
查询数据库索引就像是查询一个打印的电话号码簿。键的概念就是那些经过良好排序的所有条目。在一个有序数据集中查找数据是很快且容易的,因为排序的序号决定了每一条目的位置。
然而,数据库索引要比打印的电话号码簿复杂得多,因为它需要承担不断的变化。为每一个变化更新号码簿是不可能的,原因很简单,因为没有空间在现有条目之间添加新条目。号码簿通过将累积的更新只在下一次打印时来处理而绕过这一问题。但SQL数据库不可能等待那么长时间。它必须立即处理insert,delete和update语句,并且在避免移动大量数据的条件下保持索引顺序。
数据库通过关联两种数据结构来满足这一挑战,它们是双向链表和搜索树。这两种数据结构可以解释大多数数据库性能特征。
1. 索引叶子结点
索引的根本目的是为了提供一个索引数据的有序表现。然而,由于insert语句需要移动后面的条目以为新条目腾出空间,所以不可能顺序存储数据。移动大量数据是非常耗时的,所以insert语句执行很慢。这一问题的解决方案就是建立一个独立于内存中物理顺序的逻辑顺序。
逻辑顺序通过双向链表建立。每一个结点都有两个相邻条目的链接,很像一个链条。通过更新两个已有结点的链接以指向新结点以将这个新结点插入在二者之间。新结点的物理顺序无关紧要,因为双向链表维持了它的逻辑顺序。
数据结构之所以称为双向链表,是因为每个结点都指向了它的前一个和后一结点。这使得数据库能够按需向前或向后读取索引。因此插入新的条目时将无需移动大量数据——仅需改变一些指针就可以了。
双向链表也用于很多编程语言中的集合(容器)。
| 编程语言 | 名称 |
|---|---|
| Java | java.util.LinkedList |
| .NET Framework | System.Collections.Generic.LinkedList |
| C++ | std::list |
数据库用双向链表来连接所谓的索引叶子结点。每一叶子结点都保存在数据库块或页中,这是数据库中的最小存储单元。所有索引块大小相同——一般是数K字节。数据库尽最大可能地使用每一个块上的空间,以尽可能多地存储索引条目。这意味着索引顺序维持在两个不同的级别上:每一个叶子结点上的索引条目和在叶子结点彼此之间使用双向链表。
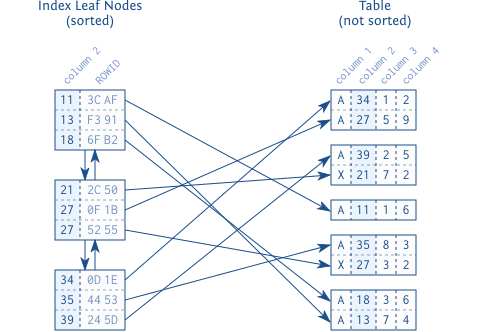
图1.1展示了索引叶子结点和它们到表数据的连接。每一个索引条目由被索引的列(键,column 2)和对应行(通过ROWID或RID)的引用构成。与索引不同,表数据以堆结构存储,不经过排序。存储在块中的行之间没有关系,块与块之间也没有连接。
2. 搜索树(B-树)使索引更快
索引叶子结点以任意顺序存储——磁盘上的位置并不对应按照索引顺序的逻辑位置。它像是一本打乱了页的电话号码簿。如果你查询“Smith”,但打开号码簿的位置是“Robinson”,它决不意味着Smith就在Robinson后面。数据库需要第二种结构来在打乱的号码簿中快速查找条目,即平衡搜索树(Balanced Search Tree)——简称:B-树。
图1.2 B-树结构
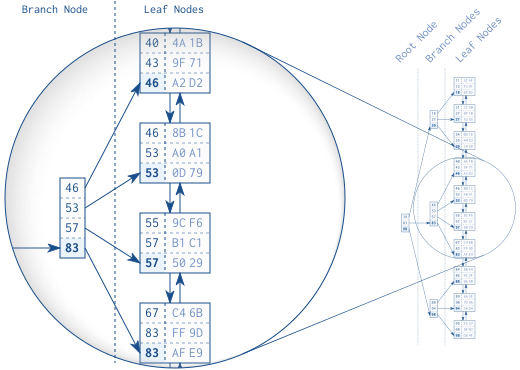
图1.2显示了一个具有30个条目的索引。双向链表在叶子结点之间建立了逻辑顺序。根结点和分支结点支持在叶子结点之间进行快速查询。
上图放大部分是一个分支结点和其引用的叶子结点。分支结点的每个条目对应叶子结点中的最大值。以第一个叶子结点为例:它的最大值是46,因此46被保存为对应分支结点中的一个条目。其他叶子结点一样,所以最终分支结点的条目是46、53、57和83。按照这一模式,直到全部叶子结点被分支结点覆盖,就创建了一个分支层。
类似地,下一层也会创建,但是在第一个分支层之上。重复这一步骤直到所有的键都纳入到一个单独结点上,即根结点。这一数据结构就是平衡搜索树,因为树的深度在每一个位置都相待,根结点与叶子结点之间的距离处处相同。
注意:B-树是平衡树不是二叉树
一旦创建,数据库就会自动维护索引。每一个insert、delete和update都会应用到索引以保持树的平衡,因此对于写操作就会产生维护开销。Chapter 8, “Modifying Data”对此有更详细的解释。
图1.3 B-树遍历
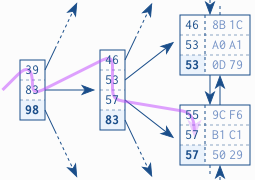
图1.3 显示一个索引片段以演示一个对键“57”的查询。树遍历从根结点开始。按升序处理每一条目,直到出现大于或等于(>=)搜索荐的值(57)。图中是条目83。数据库跟随引用到达对应的分支结点,然后重复上面过程直到树遍历到达一个叶子结点。
重要:B-树遍历使得数据库能够快速找到一个叶子结点。
B-树遍历是一个非常高效的操作,所以我把它看作是索引的第一生产力。即使是在巨大的数据集上,它也能立即完成。主要是因为树的平衡,使得可以用相同的步数来访问所有元素,其次因为树的深度是呈对数增长的。这意味着树的深度与叶子结点的数量相比,增长非常缓慢。真实世界中,对于具有数百万条记录的索引,树深度只有4或5。深度为6的树几乎看不到。以下对此进行了更详细的描述。
在数学中,给定底的一个数的对数是这个底的指数或幂。
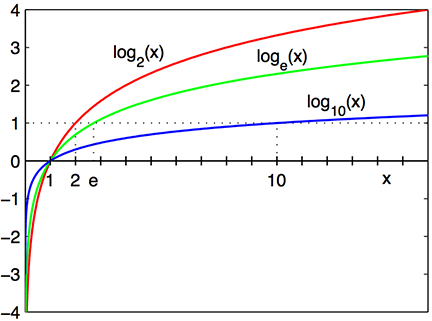 ]
]在搜索树中,对数的底对应每个分支结点中的条目数量,幂对应树的深度。图1.2中的索引一个结点持有最多4个条目,树的深度是3。这意味着该索引最多可以持有64(43)个条目。如果它增长一层,将可以持有256(44)个条目。树每添加一层,索引条目的最大数就扩大4倍。对数与此函数相反。因此树深度是log4(索引条目数)。
| 树深度 | 索引条目 | 树深度 | 索引条目 | 树深度 | 索引条目 |
|---|---|---|---|---|---|
| 3 | 64 | 6 | 4096 | 9 | 262144 |
| 4 | 256 | 7 | 16384 | 10 | 1048576 |
| 5 | 1024 | 8 | 65536 |
对数增长使得图1.2中的索引能够在深度为10的树中查询100万条记录,但真实世界的索引更高效。影响树的深度,从而影响查询性能的主要因素就是每一结点的条目数量。这个数量——从数学意义上讲——对应对数的底。底越大,树深度就越浅,遍历就越快。
数据库最大程度地利用这一概念,每一结点保存尽可能多的条目——通常是数百个。这意味着索引每增加一层,就可以多支持100倍的条目数。